0. 前言 有幸,在软件可靠性课程的实验中,被要求实现BP神经网络模型。虽然,我觉得这门课程搭配这样的实验很无厘头,但正好趁这个机会,重新学习一下神经网络知识。学校的课程设计总归是不太令人满意的,但只要能学到有益的知识,就是赚到了。至于学分、绩点多少,就无关紧要了。
BP神经网络模型简介:
BP神经网络模型是1986年由Rumelhart和McClelland为首的科学家提出的概念,是一种按照误差逆向传播算法训练的多层前馈神经网络,是目前应用最广泛的神经网络。
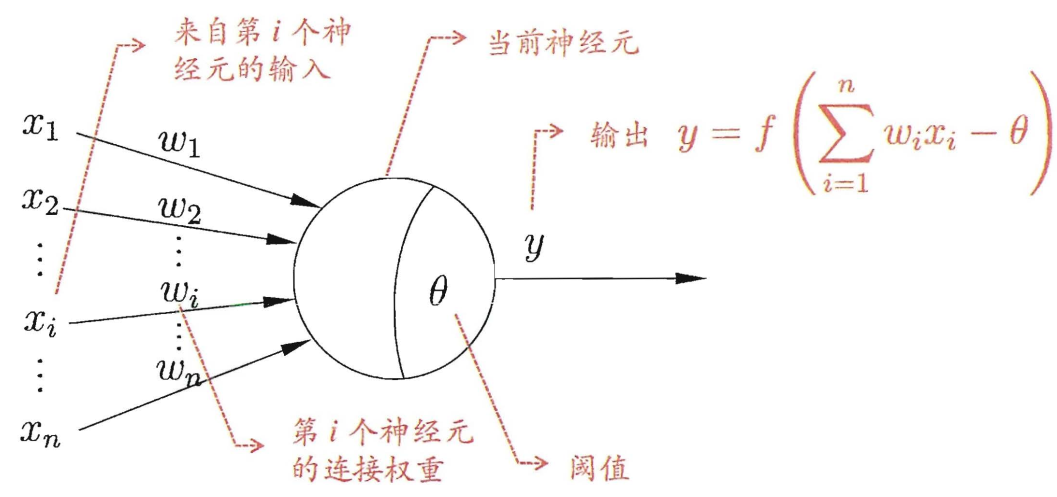
1. 神经网络基本模型 1.1. 单神经元模型
其中,f(x)函数为神经元输出经过的激活函数 。
常见的激活函数有:
$$sigmoid(x) = \frac{ 1 }{ 1+exp(-x) }$$
$$
ReLU(Rectified Linear Unit)函数
$$
值得注意的是,激活函数大多为非线性函数 。原因在于:
线性函数的问题在于,不管如何加深层数,总是存在与之等效的“无隐藏层的神经网络”。为了具体地(稍微直观地)理解这一点,我们来思考下面这个简单的例子。这里我们考虑把线性函数 h(x) = cx 作为激活函数,把y(x) = h(h(h(x)))的运算对应3层神经网络A。这个运算会进行y(x) = c × c × c × x的乘法运算,但是同样的处理可以由y(x) = ax(注意,a = c^3)这一次乘法运算(即没有隐藏层的神经网络)来表示。
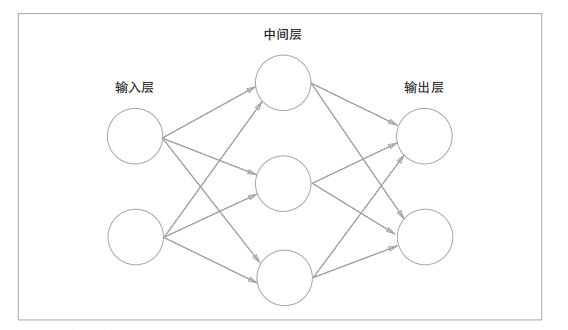
1.2. 多层神经网络
当神经网络有多层时,中间的层称为中间层或隐藏层。隐藏层的输入为上一层的输出,隐藏层的输出为下一层的输入,对隐藏层的输出同样需使用激活函数 。输入层则一般不需要经过激活函数。
值得注意的是,一个神经元的输出会传递到下一层的每个 神经元上。
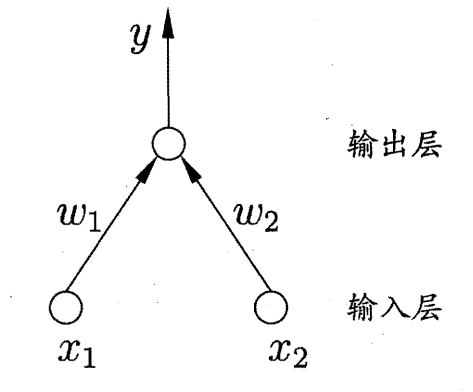
1.3. 神经网络学习过程 以感知机(由两层神经元组成)为例:
对于训练样例$(X, y)$,其中$X={x_1, x_2}$,当前神经网络的输出为$\hat{y}$。假定输出层的激活函数为阶跃函数,其数学推导为:
$$\hat{y} = f(w_1x_1 + w_2x_2 - \theta)$$
将实际值$y$与预测值$\hat{y}$进行数学比较,从而得出各权值$w_i$和阈值$\theta$的误差,从而更新相应的权值和阈值:
$$\Delta w_i = \eta(y - \hat{y})x_i$$
$$w_i \leftarrow w_i + \Delta w_i$$
其中,$\eta \in (0,1)$,称为学习率。当$\hat{y}$与$y$相等,或者之差足够小时,则可认定为训练成功。
2. BP误差反向传播算法 2.1. 算法推导 BP神经网络的数学推导过程相对简单,读者切不可望而却步。
更详细内容请参考西瓜书第5章——神经网络。
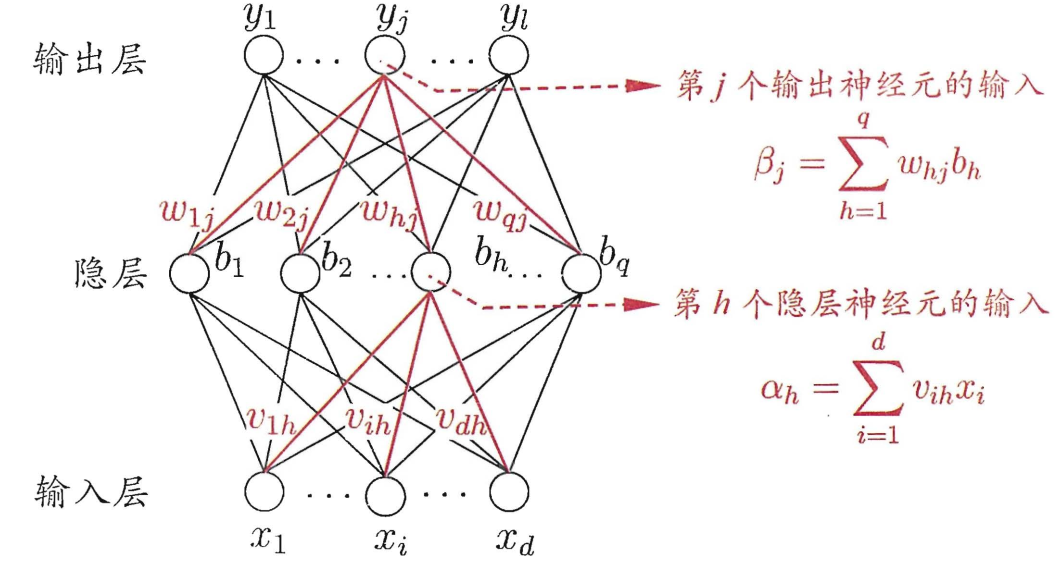
以三层神经网络为例:
注 :输入层到隐藏层的阈值为$\gamma_h$,隐藏层到输出层的阈值为$\theta_j$,激活函数$f(x)$都为$Sigmoid$函数。
假定,对于一组样例$(X_k, Y_k)$,神经网络输入为$X_k = (x_1^k, x_2^k,…, x_d^k)$,输出为$\hat{Y}_k = (\hat{y}_1^k, \hat{y}_2^k,…, \hat{y}_l^k)$。
隐藏层输出为:
$$b_h = f(\alpha_h - \gamma_h)$$
输出层输出为:
$$\hat{y}_j^k = f(\beta_j - \theta_j)$$
那么,神经网络在当前样例$(X_k, Y_k)$上 的均方误差 为:
$$E_k = \frac{1}{2}\sum_{j=1}^l(\hat{y}_j^k-y_j^k)^2$$
根据均方误差结果,基于梯度下降 策略,以目标的负梯度方向对隐层到输出层的权值参数$\Delta w_{hj}$进行调整。给定学习率,有:
$$\begin{aligned}
$$\begin{aligned}j^k}{\partial \beta_j}\cdot\frac{\partial \beta_j}{\partial w {hj}}
显然:
$$\frac{\partial E_k}{\partial \hat{y}_j^k} = \hat{y}_j^k-y_j^k$$
根据图例中$\beta_j$的函数,又显然:
$$\frac{\partial \beta_j}{\partial w_{hj}} = b_h$$
再根据$Sigmoid$函数的定义:
$$f^\prime(x) = f(x)(1-f(x))$$
则:
$$\frac{\partial \hat{y}_j^k}{\partial \beta_j} = \hat{y}_j^k(1-\hat{y}_j^k)$$
综上可得:
$$\Delta w_{hj} = -\eta(\hat{y}_j^k-y_j^k)\hat{y}_j^k(1-\hat{y}_j^k)b_h$$
令:
$$g_j = \hat{y}_j^k(y_j^k-\hat{y}_j^k)(1-\hat{y}_j^k)$$
最终:
$$\Delta w_{hj} = \eta g_j b_h$$
进而,我们可以对隐藏层到输出层的阈值$\theta_j$进行调整:
$$\begin{aligned}
同理,我们可以得到输入层到隐藏层的权值和阈值误差为:
$$\begin{aligned}
其中:
$$e_h = b_h(1-b_h)\sum_{j=1}^l w_{hj}g_j$$
2.2. 梯度下降的理解 何为梯度?
首先,它是一个向量。
其次,它的定义为:设可微函数$f(x,y,z)$,对于函数上的某一个点$P(x,y,z)$,${\frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}, \frac{\partial f}{\partial z}}$则是该函数在$P$点的梯度。
通俗来讲,函数某一点的梯度,就是该点的斜率,该点变化率最大的方向。而负梯度,则是该点能最快接近函数极小值的方向。
那么,何为梯度下降 呢?
梯度下降则是,沿当前点的负梯度方向变化:$x \leftarrow x - \gamma \nabla$,其中$\gamma$为步长。如果步长足够小,则可以保证每一次迭代都在减小,但可能导致收敛太慢;如果步长太大,则不能保证每一次迭代都减少,也不能保证收敛。
以函数$f(x) = x^2$为例:
其梯度函数为$\nabla = 2x$。
点$p(1,1)$处的梯度为$2$。
设步长为0.2,点$p$处进行梯度下降后,下一个点则为$(0.6, 0.64)$。
在BP神经网络中,采用梯度下降则是为了以最快速度调整参数,将误差降到极小(此处涉及到极小与最小的数学问题,有兴趣者可以看看西瓜书)。
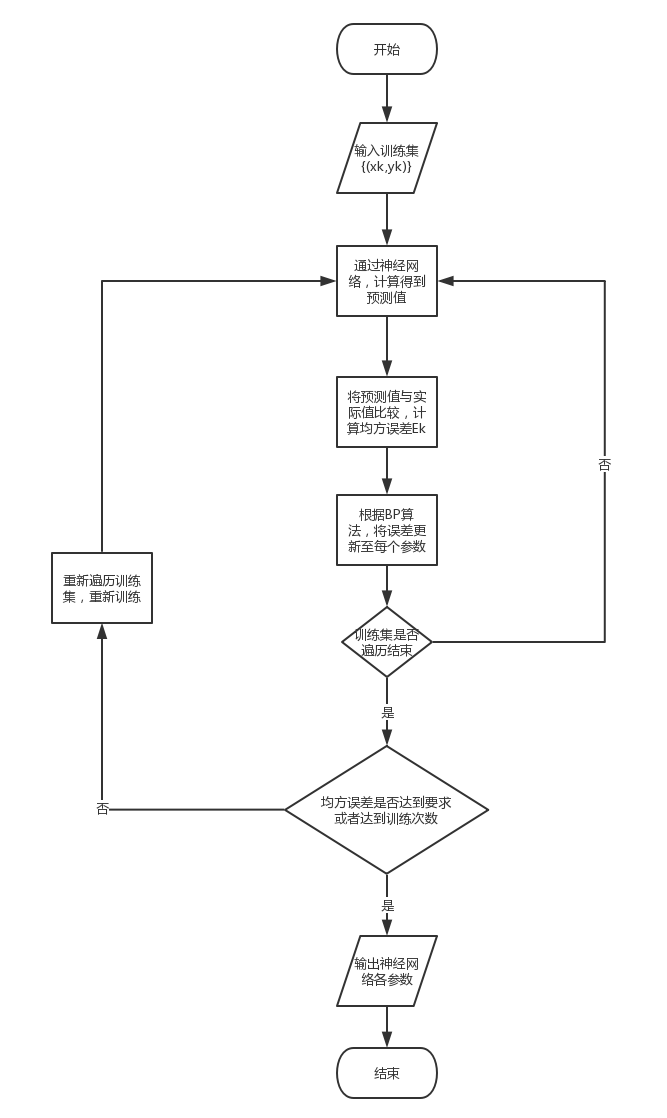
2.3. 算法步骤
2.4. 算法流程
2.5. 算法实现 编写一个三层神经网络的BP类,在构造函数中初始化神经网络:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 import randomimport matplotlib.pyplot as pltimport mathfrom tensorflow.examples.tutorials.mnist import input_dataimport numpy as np''' 三层神经网络模型,包含:输入层、隐层、输出层 ''' class BP : ''' 构造函数,初始化三层神网络的各参数 Args: x_count: 输入层神经元个数 mid_count: 隐层神经元个数 y_count: 输出层神经元个数 eta: 学习率 train_count: 最大训练次数 precision: 误差精度 ''' def __init__ (self, x_count, mid_count, y_count, eta=0.3 , train_count=100 , precision=0.00001 ): self.x_count = x_count self.mid_count = mid_count self.y_count = y_count self.eta = eta self.train_count = train_count self.precision = precision self.V = [] for i in range (0 , x_count): temp = [] for j in range (0 , mid_count): temp.append(2 *random.random() - 1 ) self.V.append(temp) self.gamma = [] for i in range (0 , mid_count): self.gamma.append(2 *random.random() - 1 ) self.W = [] for i in range (0 , mid_count): temp = [] for j in range (0 , y_count): temp.append(2 *random.random() - 1 ) self.W.append(temp) self.beta = [] for i in range (0 , y_count): self.beta.append(2 *random.random() - 1 )
其次,在BP类中,编写一个训练神经网络的类方法:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 ''' 神经网络训练函数 Args: X: 列表,输入数据 Y: 列表,实际输出数据 ''' def train (self, X, Y ): if len (X) != len (Y): print ("Error: len(X) and len(Y) is unequal!!!" ) return for i in range (self.train_count): E = [] for j in range (len (X)): y_predict, mid_output = self.compute_y(X[j]) e = 0.0 mid2y_g = [] for k in range (self.y_count): e += pow (y_predict[k] - Y[j][k], 2 ) E.append(e/2 ) mid2y_g = [] for k in range (self.y_count): mid2y_g.append(y_predict[k] * (1 - y_predict[k]) * (Y[j][k] - y_predict[k])) x2mid_g = [] for k in range (self.mid_count): temp = 0 for l in range (self.y_count): temp += self.W[k][l] * mid2y_g[l] x2mid_g.append(mid_output[k] * (1 - mid_output[k]) * temp) for k in range (self.mid_count): for l in range (self.y_count): self.W[k][l] += self.eta * mid2y_g[l] * mid_output[k] for k in range (self.y_count): self.beta[k] -= self.eta * mid2y_g[k] for k in range (self.x_count): for l in range (self.mid_count): self.V[k][l] += self.eta * x2mid_g[l] * X[j][k] for k in range (self.mid_count): self.gamma[k] -= self.eta * x2mid_g[k] E_sum = 0.0 for e in E: E_sum += e E_sum /= len (E) print (E_sum) if E_sum < self.precision: break
该函数用到的类方法如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 ''' Sigmoid激活函数 Args: x Returns: y: sigmoid(x) ''' def sigmoid (self, x ): return 1 / (1 + math.exp(-x)) ''' 计算一组预测值 Args: x: 列表,一组多元或一元的输入数据 Returns: y: 列表,一组多元或一元的输出数据 mid_output: 列表,隐层的输出数据 ''' def compute_y (self, x ): mid_input = [] for i in range (self.mid_count): temp = 0 for j in range (self.x_count): temp += self.V[j][i] * x[j] mid_input.append(temp) mid_output = [] for i in range (self.mid_count): mid_output.append(self.sigmoid(mid_input[i] - self.gamma[i])) y_input = [] for i in range (self.y_count): temp = 0 for j in range (self.mid_count): temp += self.W[j][i] * mid_output[j] y_input.append(temp) y = [] for i in range (self.y_count): y.append(self.sigmoid(y_input[i] - self.beta[i])) return (y, mid_output)
最后,在BP类中,编写一个基于神经网络进行预测的类方法:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 ''' 神经网络预测函数 Args: X: 列表,输入数据 Returns: Y_predict: 列表,预测输出数据 ''' def predict (self, X ): Y_predict = [] for x in X: y_predict, _ = self.compute_y(x) Y_predict.append(y_predict) return Y_predict
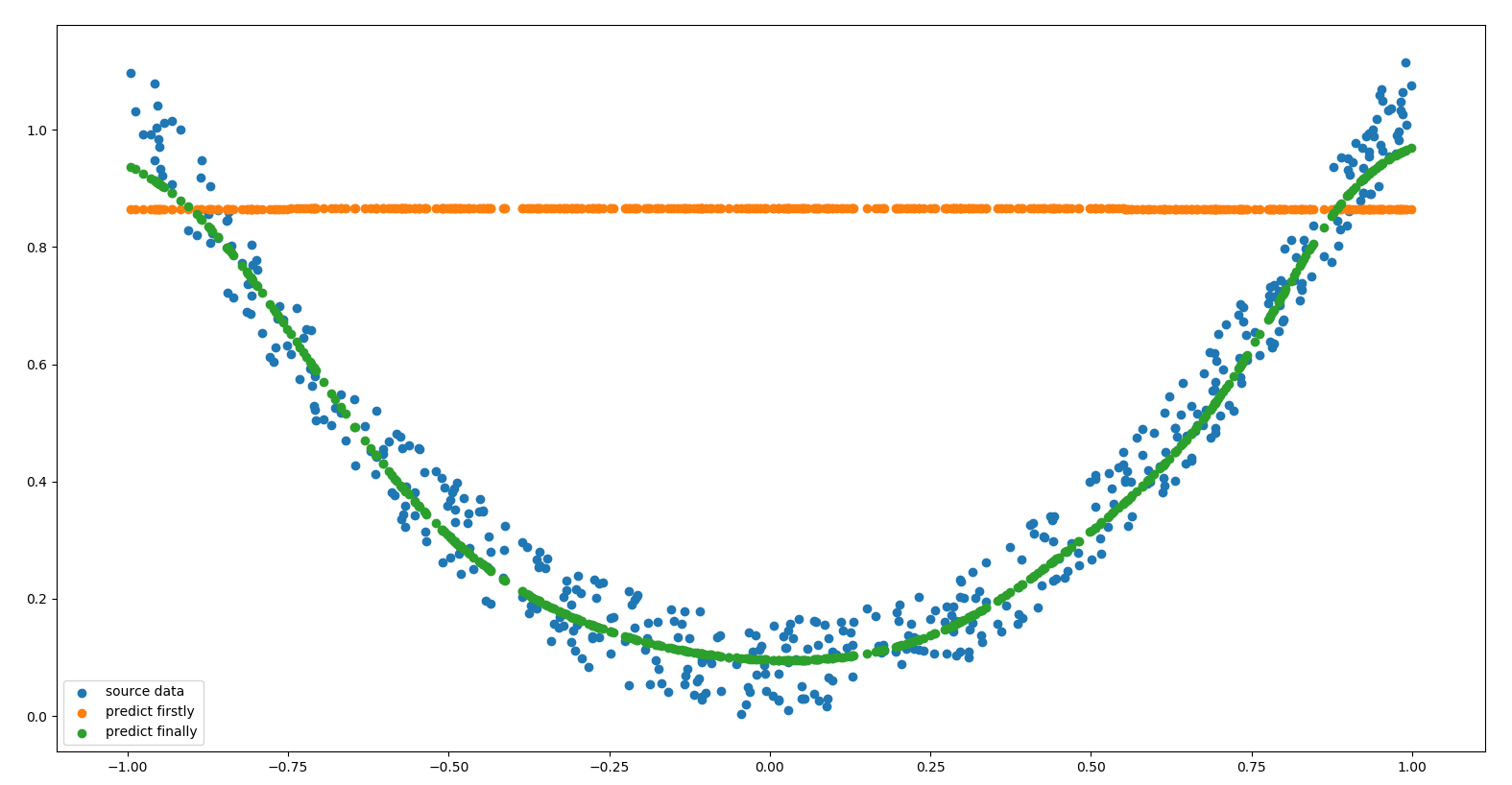
2.6. 算法检验 2.6.1. 预测$y=x^2$模型 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 ''' 预测 y=x^2 函数模型 ''' data_count = 500 X = [] for i in range (data_count): X.append([2 *random.random() - 1 ]) Y = [] for i in range (data_count): noise = random.random() / 6 Y.append([pow (X[i][0 ], 2 ) + noise]) plt.scatter(X, Y, label='source data' ) bp = BP(x_count=1 , mid_count=10 , y_count=1 , eta=0.3 , train_count=1000 , precision=0.00001 ) Y_predict = bp.predict(X) plt.scatter(X, Y_predict, label='predict firstly' ) bp.train(X, Y) Y_predict = bp.predict(X) plt.scatter(X, Y_predict, label='predict finally' ) plt.legend() plt.show()
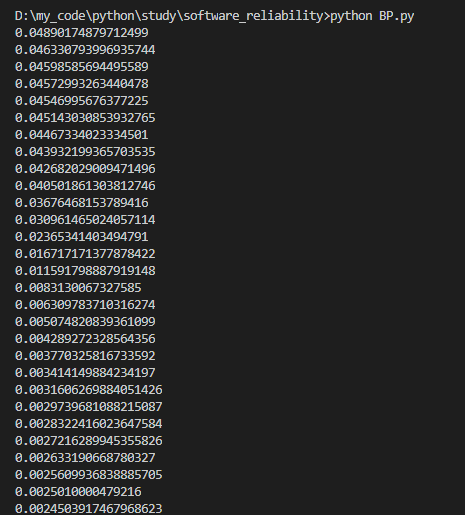
控制台输出每一轮训练后的累计误差如下:
显示的原数据与预测数据对比图如下:
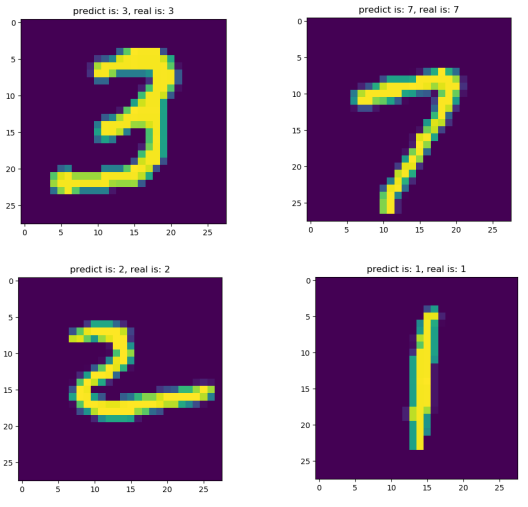
2.6.2. 预测mnist手写数字图片数据集 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 ''' 预测mnist数字图片数据集 ''' mnist = input_data.read_data_sets("MNIST_data/" , one_hot=True ) X_train = mnist.validation.images[:100 ].tolist() Y_train = mnist.validation.labels[:100 ].tolist() X_test = mnist.validation.images[100 :120 ].tolist() Y_test = mnist.validation.labels[100 :120 ].tolist() bp = BP(x_count=784 , mid_count=10 , y_count=10 , eta=0.3 , train_count=100 , precision=0.001 ) bp.train(X_train, Y_train) Y_predict = bp.predict(X_test) for i in range (len (Y_predict)): max_pos = 0 Max = 0 for j in range (len (Y_predict[i])): if Y_predict[i][j] > Max: max_pos = j Max = Y_predict[i][j] image = X_test[i] image = np.array(image).reshape(28 , 28 ) plt.imshow(image) plt.title('predict is: {}, real is: {}' .format (max_pos, Y_test[i].index(1 ))) plt.ion() plt.pause(3 ) plt.close()
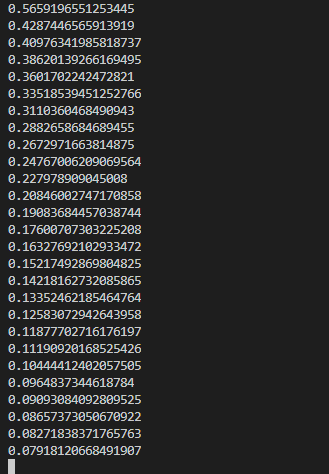
控制台输出每一轮训练后的累计误差如下:
挑选4张预测结果图片,如下:
3. 参考